math
max
max( a, b )| max | "maximum" |
| a | a number |
| b | a number |
The max( a, b ) function is used to compare two numbers a and b, and it returns the greater of the two numbers.
![]()
For example, if we call max(5, 8), the function will compare the two arguments and determine that 8 is the greater value. Therefore, it will return 8.
greater = max(5,8)
print(greater) --prints 8Similarly, if we call max(-3, 0), the function will return 0 since 0 is greater than -3.
greater = max(0,-3)
print(greater) --prints 0![]()
1173
11 Apr 2023
min
min( a, b )| min | "minimum" |
| a | a number |
| b | a number |
The min( a, b ) function is used to compare two numbers a and b, and it returns the lesser of the two numbers.
![]()
For example, if we call min(4, 18), the function will compare the two arguments and determine that 4 is the lesser value. Therefore, it will return 4.
lesser = min(4,18)
print(lesser) --prints 4Similarly, if we call min(-5, 1), the function will return -5 since -5 is less than 1.
lesser = min(1,-5)
print(greater) --prints -5![]()
1060
11 Apr 2023
mid
mid( a, b, c )| mid | "middle" |
| a | a number |
| b | a number |
| c | a number |
The mid(a, b, c) function is used to determine the number in the middle of three given numbers a, b, and c.
![]()
For example, if we call mid(10, 4, 20), the function will compare the three arguments and determine that 10 is the middle value. Therefore, it will return 10.
middle = mid(10, 4, 20)
print(middle) --prints 10Using mid() to Create Limits
One way to use this function in your game, is to make sure a number stays within a certain range of numbers. For example, keeping a player within the screen's width. The player's x coordinate can be limited to the screen's left side of 0 and right side of 127.
If we call mid(), with the arguments of the player x, and the minimum and maximum of the allowed range, then the player's x will be limited to those minimum and maximum values. Here's an example:
left=0
right=127
x=60 --player
function _update()
--player movement
if btn(⬅️) then x-=1 end
if btn(➡️) then x+=1 end
x= mid(left,right,x)
end
function _draw()
spr(player_sprite,x,120)
end
Notice how the player does move off the right side of the screen. This is to demonstrate that you need to remember that a sprite's X and Y coordinates are for the top-left corner of the sprite. So using mid above is still working to limit the player's X on the screen, because it is not letting the player's left side leave the range of the screen.
To fix this, remember to adjust the right side limit by the sprite's width like so:
x= mid(left,right-8,x)
![]()
1514
1 Jan 2025
flr
flr( a )| flr | "floor" |
| a | a number |
The flr( a ) function is used to round down the given number, a, and return an integer (whole number).
![]()
For example, if we call flr(1.99), the function will round down to the nearest whole number and return that value. Therefore, it will return 1.
value = flr(1.99)
print(value) --prints 1If we pass a negative number, for example flr(-5.3), the function will return -6 since it is the nearest whole number down.
value = flr(-5.3)
print(value) --prints -6There are many reasons you will want to "floor" a number. One common use is with the time() function, which almost always returns a decimal value, but you may want to simply know the number of seconds passed without any decimal places.
function _draw()
cls()
millisec = time()
sec = flr( millisec )
print("time="..millisec,20,40,8)
print("floored="..sec,20,60,12)
end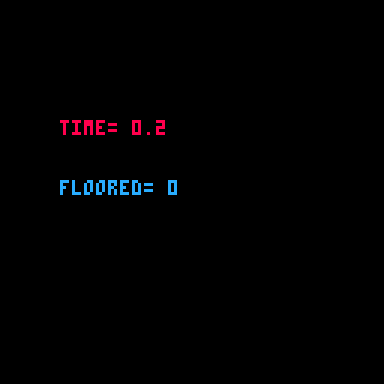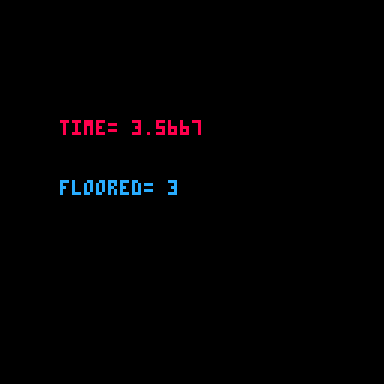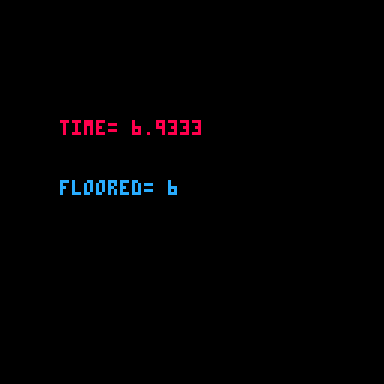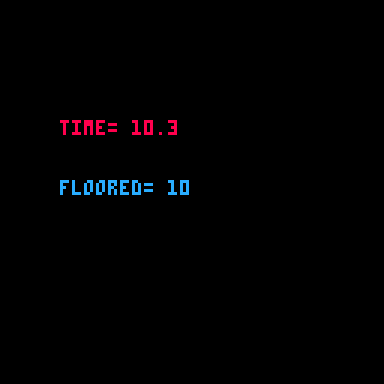
![]()
Shorthand
It is common to want to floor a number after dividing, and there is a shorthand for that, the backslash ( \ ).
--longform
a = flr(10/3)
--shorthand
b = 10\3It is also common to want to floor a random number.
--longform
a = flr( rnd(10) ) --integer range 0-9
--shorthand
b = rnd(10)\1 --integer range 0-9![]()
1680
12 May 2023
ceil
ceil( a )| ceil | "ceiling" |
| a | a number |
The ceil( a ) function is used to round up the given number, a, and return the nearest larger whole number.
![]()
For example, if we call ceil(4.02), the function will round up to the nearest whole number and return that value. Therefore, it will return 5.
value = flr(4.02)
print(value) --prints 5If we pass a negative number, for example flr(-8.6), the function will return -8 since it is the nearest larger whole number.
value = flr(-8.6)
print(value) --prints -8There are many reasons you may want to use ceil(). For example, in games that involve damage, health, or currency, you might want to ensure that these values are always rounded up to the nearest whole number. For example, if a character takes 3.2 points of damage, you might use ceil() to round that up to 4 points of damage because of a small powerup.
![]()
1220
22 Nov 2023
cos
cos( x )| cos | "cosine" |
| x | a number |
The cos( x ) function is used to return the cosine of the number provided.
An example from the manual shows us how to draw a rotating dial using cos() and sin():
function _draw()
cls()
circ(64, 64, 20, 7)
x = 64 + cos(t()) * 20
y = 64 + sin(t()) * 20
line(64, 64, X, Y)
end
We've slowed it down and added some more details to show what is happening here:
function _draw()
cls()
circ(64, 64, 20, 5)
x = 64 + cos(t()/5) * 20
y = 64 + sin(t()/5) * 20
line(64, 64, x, 64,8) -- x-axis cosine
line(64, 64, 64, y,11) -- y-axis sine
line(64, 64, x, y,6) -- main dial line
pset(x, y,12) -- (x,y) point
end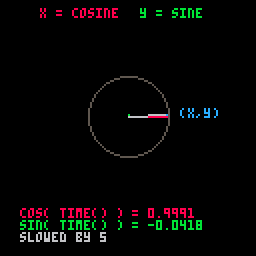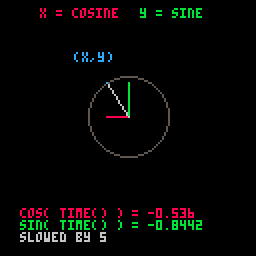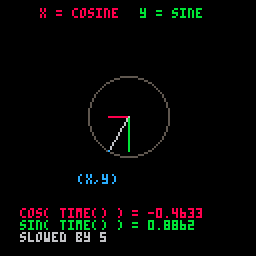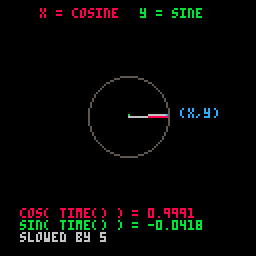
![]()
1529
4 Sep 2023
sin
sin( x )| sin | "sine" |
| x | a number |
The sin( x ) function is used to return the sine of the number provided.
An example from the manual shows us how to draw a rotating dial using cos() and sin():
function _draw()
cls()
circ(64, 64, 20, 7)
x = 64 + cos(t()) * 20
y = 64 + sin(t()) * 20
line(64, 64, X, Y)
end
We've slowed it down and added some more details to show what is happening here:
function _draw()
cls()
circ(64, 64, 20, 5)
x = 64 + cos(t()/5) * 20
y = 64 + sin(t()/5) * 20
line(64, 64, x, 64,8) -- x-axis cosine
line(64, 64, 64, y,11) -- y-axis sine
line(64, 64, x, y,6) -- main dial line
pset(x, y,12) -- (x,y) point
end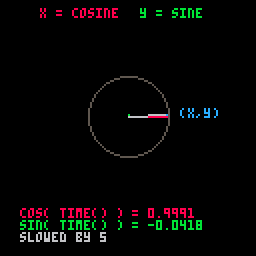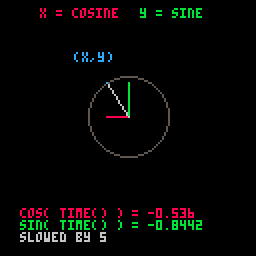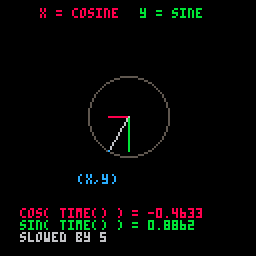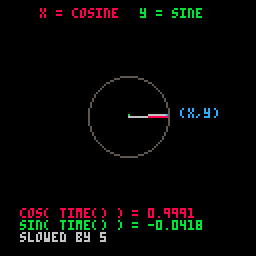
![]()
1583
4 Sep 2023
atan2
atan2( dx, dy )| atan2 | "2-argument arctangent" |
| dx | a number |
| dy | a number |
The atan2( ) function is used to return the angle of the numbers provided.
An example from the manual shows us how to get and draw the angle between two points using atan2:
X=20 Y=30
FUNCTION _UPDATE()
IF (BTN(0)) X-=2
IF (BTN(1)) X+=2
IF (BTN(2)) Y-=2
IF (BTN(3)) Y+=2
END
FUNCTION _DRAW()
CLS()
CIRCFILL(X,Y,2,14)
CIRCFILL(64,64,2,7)
A=ATAN2(X-64, Y-64)
PRINT("ANGLE: "..A)
LINE(64,64,
64+COS(A)*10,
64+SIN(A)*10,7)
END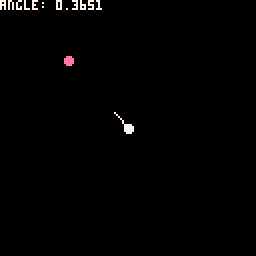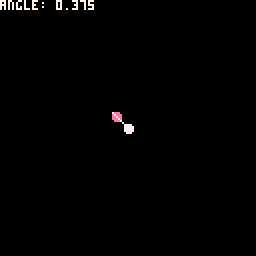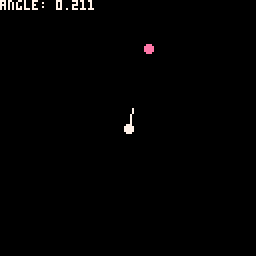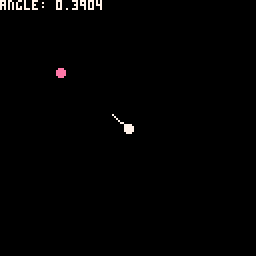
We've added some more details to show what is happening here:
angle = atan2( x1-x2, y1-y2 )Using the angle found with atan2() and combining it with cos(angle) and sin(angle), we are able to draw the line that always points from one point to the other.
![]()
1511
4 Sep 2023
sqrt
sqrt( a )| sqrt | "square root" |
| a | a number |
The sqrt( a ) function is used to return the square root of the number provided.
For example, let's first square a number, then use sqrt() to reverse it:
--two ways to square a number
a = 4*4 --16
b = 4^2 --16
c = sqrt(b) --square root
print(c) --4![]()
1169
12 May 2023
abs
abs( a )| abs | "absolute" |
| a | a number |
The abs( a ) function is used to return the absolute number of the number given.
To understand what an absolute value is, imagine you are standing at any point on a number line and you want to know how far away from zero you are, no matter which side of zero you are standing (positive or negative). This is why the absolute value will always be a positive number.
For example:
a = abs(5) --5
b = abs(-42) --42
c = abs(3.75) --3.75
d = abs(-6.25) --6.25![]()
1255
31 Jul 2024
rnd
rnd( a )| rnd | "random" |
| a | a number or table |
The rnd( a ) function is used to return a random number within the range of 0 up to but not including the number given.
Get Random Number
For example:
a = rnd(5) --range: 0-4.9999
b = rnd(20) --range: 0-19.9999
c = rnd(500) --range: 0-499.9999To get a random integer (whole number) use flr() with rnd() like this:
d = flr( rnd(10) ) --range: 0-9 integers
--shorthand floor
e = rnd(10)\1 --range: 0-9 integersGet Random Table Value
You can also pass a table to the rnd() function to get a random value from the table:
table = { 4, 6, 8, 10 }
rnd(table) --4, 6, 8, or 10The table must have numbered keys because the function will find a random integer between 1 and the total count of the table and return the value stored at that table index. There is also a shorthand of providing the table itself in replace of the parentheses:
table={ 1, 3, 4, 10 }
--longform
table[ 1 + flr( rnd(#table) ) ]
--shorthand
rnd{ 1, 3, 4, 10 }This can be useful for specifying a list of certain possible values, such as the spawn zone of an enemy, or the color numbers of a rectangle:
colors = { 8, 9, 12, 1, 4 }
rectfill( 40,50,60,70,rnd(colors) )
Notice that the color numbers in the table can be in any order.
![]()
1976
12 May 2023
srand
srand( seed )| s | (seed) a number to use as a seed value |
| rand | "random" |
The srand() function is used to seed the random number generator: rnd(). In computer programming, a random number generator is not truly random, it is actually a deterministic algorithm that produces a sequence of seemingly random numbers. Every time a PICO-8 cart runs, the rnd() function uses a different seed value to begin generating its sequence of numbers.
By providing a seed value to srand(), you can control and reproduce the same sequence of random numbers.
For example:
--random every time
print( rnd(10) ) --unpredictable
print( rnd(10) ) --unpredictable
print( rnd(10) ) --unpredictable
--seeded random
srand(5)
print( rnd(10) ) --3.6121
print( rnd(10) ) --7.4159
print( rnd(10) ) --9.0311
--same seed, same results
srand(5)
print( rnd(10) ) --3.6121
print( rnd(10) ) --7.4159
print( rnd(10) ) --9.0311This could be used with a random level generator to reproduce the same level or sequence of levels in your game.
Since rnd() can also be used to get values from tables at random, you can use srand() to make the table value selection more predictable and in a specific sequence.
table = { "a", "b", "c", "d" }
--random
print( rnd(table) ) --unpredictable
--seeded random
srand(5)
print( rnd(table) ) --a
print( rnd(table) ) --c
print( rnd(table) ) --d
--same seed, same results
srand(5)
print( rnd(table) ) --a
print( rnd(table) ) --c
print( rnd(table) ) --d![]()
1968
19 Aug 2023



