collision:
Line to Line

Storing Line Data

First, we need to store the coordinates of two line segments. Each line segment needs two endpoints, so we'll use 4 coordinates per line: (x1,y1) and (x2,y2). We can store these as tables:

--create two line segments as object tables
line1 = { x1=20, y1=20, x2=120, y2=100 }
line2 = { x1=80, y1=20, x2=100, y2=120 }

Now we have one line segment from (20,20) to (120,100), and another from (80,20) to (100,120). To access the values from the tables, we use dot notation (See Table Shorthand).

--get values out of line tables
print( line1.x1 )  -- 20
print( line2.x2 )  -- 100

The Mathematical Approach

To check if two line segments intersect, we need to verify that:

1. The endpoints of line 1 are on opposite sides of line 2

2. The endpoints of line 2 are on opposite sides of line 1

If both conditions are true, the lines must intersect somewhere between their endpoints.

We use the cross product formula to determine which side of a line a point is on. The cross product gives us a value that indicates orientation:

• Positive value means the point is on one side
• Negative value means the point is on the other side
• Zero means the point is exactly on the line

We use PICO-8's sgn() function to get the sign (-1, 0, or 1) of each cross product:

--check which side of line1 each endpoint of line2 is on
d1 = sgn((line1.x2-line1.x1)*(line2.y1-line1.y1)-(line1.y2-line1.y1)*(line2.x1-line1.x1))
d2 = sgn((line1.x2-line1.x1)*(line2.y2-line1.y1)-(line1.y2-line1.y1)*(line2.x2-line1.x1))

--check which side of line2 each endpoint of line1 is on
d3 = sgn((line2.x2-line2.x1)*(line1.y1-line2.y1)-(line2.y2-line2.y1)*(line1.x1-line2.x1))
d4 = sgn((line2.x2-line2.x1)*(line1.y2-line2.y1)-(line2.y2-line2.y1)*(line1.x2-line2.x1))

Now that we have the sign each cross product (d1, d2, d3, d4), we can make sure that the signs are not the same:

--if signs differ in both pairs, lines intersect
if d1 != d2 and d3 != d4 then
    print("lines intersect!")
end

Understanding an Expanded Version

Here's how we can write this as a complete function with clear steps:

--expanded example
function line_line_collision( line1, line2 )
    --calculate orientation of line2.p1 relative to line1
    local d1 = sgn((line1.x2-line1.x1)*(line2.y1-line1.y1)-(line1.y2-line1.y1)*(line2.x1-line1.x1))

    --calculate orientation of line2.p2 relative to line1
    local d2 = sgn((line1.x2-line1.x1)*(line2.y2-line1.y1)-(line1.y2-line1.y1)*(line2.x2-line1.x1))

    --calculate orientation of line1.p1 relative to line2
    local d3 = sgn((line2.x2-line2.x1)*(line1.y1-line2.y1)-(line2.y2-line2.y1)*(line1.x1-line2.x1))

    --calculate orientation of line1.p2 relative to line2
    local d4 = sgn((line2.x2-line2.x1)*(line1.y2-line2.y1)-(line2.y2-line2.y1)*(line1.x2-line2.x1))

    --check if endpoints are on opposite sides
    if d1 != d2 and d3 != d4 then
        return true
    else
        return false
    end
end

This function has parameters (line1, line2) and expects each line to have x1,y1,x2,y2 coordinates.

The function calculates four orientation values using cross products. The first two (d1 and d2) tell us which sides of line1 the endpoints of line2 are on. The second two (d3 and d4) tell us which sides of line2 the endpoints of line1 are on. If both pairs have different signs, the lines must cross each other.

You can call this function two ways to detect collisions:

--catch result in variable
is_colliding = line_line_collision( line1, line2 )

if is_colliding then
    print("collision detected!")
end

--directly inside of if statement
if line_line_collision( line1, line2 ) then
    print("collision detected!")
end

Example with different object names:

laser = { x1=0, y1=64, x2=128, y2=64 }
wall = { x1=64, y1=0, x2=64, y2=128 }

if line_line_collision( laser, wall ) then
    print("laser hit wall!")
end

(See more examples below in When to Use this?)

Understanding the Simplified Version

We can condense the expanded version into just these 3 lines shown at the top:

function line_line_collision(l1,l2)
  local d1=sgn((l1.x2-l1.x1)*(l2.y1-l1.y1)-(l1.y2-l1.y1)*(l2.x1-l1.x1))
  local d2=sgn((l1.x2-l1.x1)*(l2.y2-l1.y1)-(l1.y2-l1.y1)*(l2.x2-l1.x1))
  local d3=sgn((l2.x2-l2.x1)*(l1.y1-l2.y1)-(l2.y2-l2.y1)*(l1.x1-l2.x1))
  local d4=sgn((l2.x2-l2.x1)*(l1.y2-l2.y1)-(l2.y2-l2.y1)*(l1.x2-l2.x1))
  return d1!=d2 and d3!=d4
end

This works the same way but uses shorter variable names (l1 and l2 instead of line1 and line2) and combines the final check into a single return statement. The function returns true only when d1!=d2 AND d3!=d4, meaning the endpoints are on opposite sides of both lines.

Line-to-Line Collision is useful when you need to detect if line projectiles or other game objects intersect with line-based boundaries or entities in your game. This is also perfect for games with laser beams, light rays, swords or any visual effects that are drawn as thin lines but need precise collision detection.

Here are a couple mockups taking classic arcade era video games and reimagining them in PICO-8:

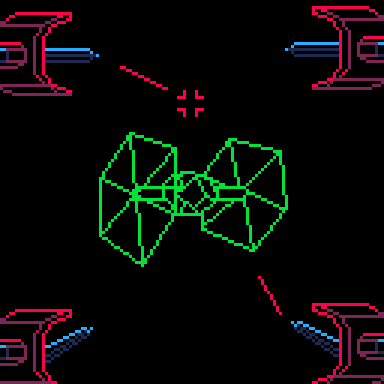
Star Wars (1983); vector graphics of lasers and wireframe enemies

The original game may have simplified this to enemy hitboxes but it is a good representation of wireframe vector sprites and lasers. When the lasers intersect with one of the lines in the enemy ship, it could count as a hit, and by drawing the ship this way, you could even know which part of the ship was hit, and remove that line to show damage at the precise location.

Great Swordsman (1984); swords as lines that could intersect to parry

Again, the original game may have simplified the attacks to high, medium, and low to determine if a player was open to an attack or defended properly. However, the game could be improved and made more realistic by allowing more interesting angles of the swords and detecting if the sword lines cross or reach the other player's body unguarded.

p1_sword = { x1=35, y1=80. x2=62, y2=100 }
p2_sword= { x1=43, y1=90, x2=60, y2=103 }

if line_line_collision( p1_sword, p2_sword ) then
    --swords cross, attack defended
end