collision:
Point to Circle
Point to Circle collision is detected by checking if the distance between the point and the center of the circle is equal to or less than the circle's radius.
No Collision
PICO-8 Collision Function
function point_circle_collision( p, c )
local dx,dy = p.x-c.x, p.y-c.y
return dx*dx + dy*dy <= c.r*c.r
endPreparing Coordinates
First, we need an easy way to store the coordinates of both a point and a circle as well as the circle's size. We can do that with 2 tables that store separate X, Y, variables. For the size of the circle, we will save a radius r, which is the distance from the center of the circle to the outer edge. Those tables (named p for the point and c for the circle) are what the above function expects.
They could be created like this:
--create object tables
p = { x=10, y=20 }
c = { x=63, y=63, r=30 }Now we have two points at their own coordinates of X and Y, and the second point will be the center of a circle with a size of r. Next we need to know how to get the values out of the tables. For example, to get the radius of the circle, we use c.r (See Table Shorthand).
--get values out of object table
print( c.r ) --prints 30Understanding the Math
The good news is you don't need to understand the details of how it works in order to use this collision function in your game. As long as you understand what you need to pass to the function and what you can expect to get returned, then you can simply trust that the math inside is working properly.
However, if you want to take more control over your code and customize how your game collision works, then understanding exactly how and why the math works the way it does is important. So we will break it down as best we can.
Overall, we want to get the distance between the point and the circle by using the coordinates of the point and the center point of the circle. We'll use some algebra and geometry here to figure out the distance. First we can easily find the difference between each point on each axis. Think of the center point of the circle at coordinates ( x1, y1 ) and the point at ( x2, y2 ).
x2 - x1 = horizontal difference
y2 - y1 = vertical difference
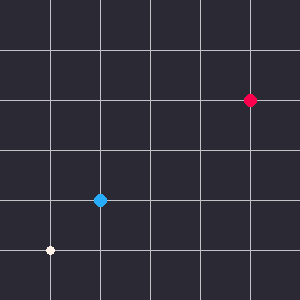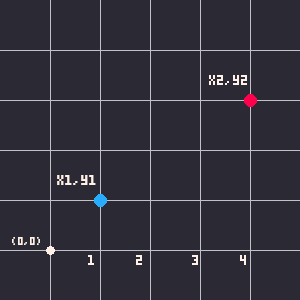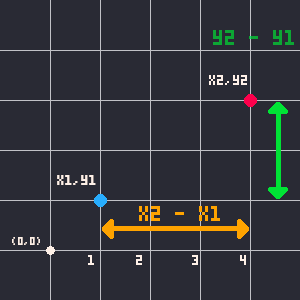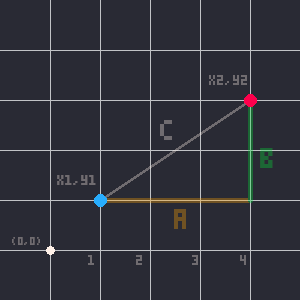
We can do this with any 2 points, imagining them as part of a right triangle, and with just subtraction we get the lengths of 2 sides of that triangle. The 3rd side is the actual distance we want to figure out. Now that we have the lengths of 2 sides of a triangle, we can figure out the third side using the Pythagorean Theorem:
c2 = a2 + b2
Basically it's just a rule about right triangles where the longest side equals the two shorter sides added together, but only when all three sides are multiplied by themselves ("squared").
We can expand that out to look like this:
c×c = a×a + b×b
And this is how we would write it in code:
c*c = a*a + b*b
Applying to our Point and Circle
Let's not get confused when we change from the math where we use A B C for the triangle sides above, back to code where we are using P and C for the point and the circle again. This is how we do the same but with our point and circle data.
| math | code | |
|---|---|---|
| Difference X = | x2 - x1 | p.x - c.x |
| Difference Y = | y2 - y1 | p.y - c.y |
In code, we can do that math to get the length of the two smaller sides, and save them in variables named dx and dy.
--difference of points
dx = p.x - c.x
dy = p.y - c.yThe next step is to multiply those sides by themselves, remember:
c*c = a*a + b*b
In the case of Point and Circle, the A is DX and the B is DY, so we want to do:
distance_squared = dx*dx + dy*dyAnd now we could simply square root the result to find the distance:
distance = sqrt( distance_squared )(PICO-8 has a built in math function for this: sqrt)
After we get the distance between the two points, we just need to compare that with the radius of the circle. If the distance is shorter than the radius, then the point must be inside the circle!
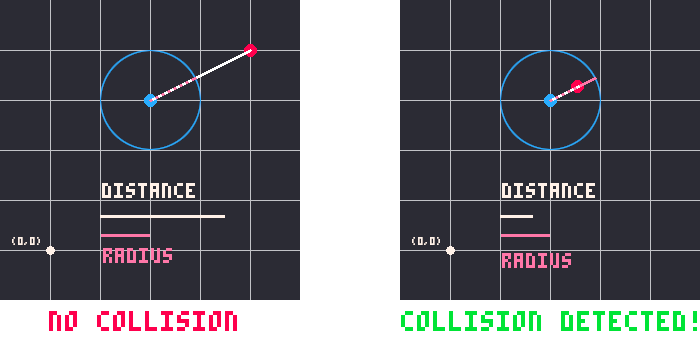
Now that you understand the math of finding the distance and comparing it with the radius, play with the demo at the top of this page to see all the pieces come together.
Understanding an Expanded Version
We can combine all of the steps above into a single function, written out clearly to show each step:
function point_circle_collision( p, c )
--get lengths of two sides; the differences
local dx = p.x-c.x
local dy = p.y-c.y
--get length of 3rd side; the distance
local distance_squared = dx*dx + dy*dy
local distance = sqrt( distance_squared )
--check if point is inside circle radius
if distance <= c.r then
return true
else
return false
end
endThis function has parameters (p,c) and it is expecting those to be objects with X, and Y keys, with the circle also having an R key for radius.
Step 1: get the differences between the points on each axis, which creates an imaginary right triangle.
Step 2: get the distance of the third side of the triangle, the actual distance of the two points.
Step 3: compare the distance and the circle's radius
Step 4: return true if the distance is shorter than the radius or false if it is longer.
You can call this function in two ways to catch the returned true or false result:
--catch result in variable
is_colliding = point_circle_collision( p, c )
if is_colliding then
print( "collided!" )
end--directly inside of if statement
if point_circle_collision( p, c ) then
print( "collided!" )
endNote that these examples use the same argument names and parameter names just for the convenience of this tutorial, but to make the difference clear, this is how the parameters of the function still uses (p,c) but the arguments when calling the function could be any object table such as:
bullet = { x=10, y=20 }
shield = { x=30, y=40, r=8 }
if point_circle_collision( bullet, shield ) then
player_health = 0
end(See more examples below in When to Use this?)
Understanding the Simplified Version
We can simplify and condense the expanded version down to just two lines:
function point_circle_collision( p, c )
local dx,dy = p.x-c.x, p.y-c.y
return dx*dx + dy*dy <= c.r*c.r
end
This works the exact same way as the expanded version because all the steps of getting the distance and comparing it to the radius is happening here too.
The first way we condensed the code is what is called multiple assignments. Where we assign more than one value to more than one variable on a single line. That way we assign dx and dy together on the first line of the function, separated by commas.
local dx,dy = p.x-c.x, p.y-c.yThe second trick we do to condense the code is to skip square rooting the distance. We do the math for finding the distance squared and immediately compare it with the circle's radius squared.
dx*dx + dy*dy <= c.r*c.r The final trick to condense it is to simply return the result of the math and the comparison, which lets us do all of that in a single line of code. It will do the math first, then compare those results, then return the comparison's result of true or false.
return dx*dx + dy*dy <= c.r*c.rPoint to Circle Collision is not used that often because it is pretty specific. You need a circular game object and something small enough that you only care about a single point.
A classic game that immediately comes to mind is the circular character of Pacman who eats single pixel pellets.

--init
pacman = { x=10, y=20, r=5 }
pellets = {} --empty table
add_pellets() --fills table with points
--update
for pellet in all( pellets ) do
--collision check
if point_circle_collision( pellet, pacman ) then
score += 100
del(pellet) --remove from game
end
endSometimes you can simplify a larger sprite down to a single point near its center. Many bullet-hell shmups will do this where the ship looks big but the hitbox is only the tiny cockpit. So the cockpit could be the point and enemy bullets could be large circles.
Or the opposite, where the player has a circular energy shield, and the enemy bullets are just points.

--init
ship = { x=10, y=20, r=5 }
shield = true
enemy_bullets = {} --empty table
add_enemy_bullets() --fills table with points
--update
for bullet in all( enemy_bullets ) do
--collision check
if shield then
if point_circle_collision( bullet, ship ) then
del(bullet) --remove from game
end
else
if point_point_collision( bullet, ship ) then
health -= 10
del(bullet) --remove from game
end
end
endMultiple Collision Check Example
This shows how you could use two different collision functions. If the shield is on, then it checks point_circle_collision(), but if the shield is off, then it checks point_point_collision() to see if the bullet hits the player cockpit instead and the player could lose health.
Another example of using Point to Circle Collision is when your game has a circular field of view and you want to determine if the player or other objects are within that space. That could be for creating fog-of-war in a strategy game, a camera's line-of-sight for a stealth game, or the light radius of a torch in an adventure game.
2401
9 Apr 2025



