collision:
Rect to Circle

Comparing Coordinates

First, we need an easy way to store the values of a rectangle and a circle. We can do that with 2 tables that store separate X, Y, and size variables. Those tables (named r for the rectangle and c for the circle) are what the above function expects.

They could be created like this:

--create object tables
r = { x=10, y=20, w=10, h=10 }
c = { x=64, y=64, r=15 }

Now we have a rectangle at its own coordinates of X and Y, with a width of w and a height of  h. We also have a circle at its own coordinates x,y and radius of r. To get the values such as x from the rectangle table r, we use r.x (See Table Shorthand).

--get values out of object table
print( r.x )   --prints 10

Find Closest Point

The first thing we want to do is find the closest point on the rectangle to the circle. If we break it down and think about it one axis at a time, it becomes pretty simple.

Let's start by considering only the X axis. A rectangle in only one dimension (width) becomes just a line with one start point and one end point, the left and right sides of the rectangle. For the circle, we only need to care about the center point and we can worry about the size of the circle later. So the circle simplifies to a single point.

That's how we simplify the problem down to only 3 points on the X axis:

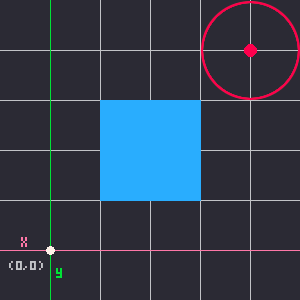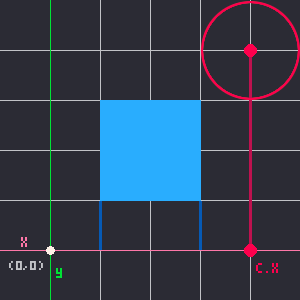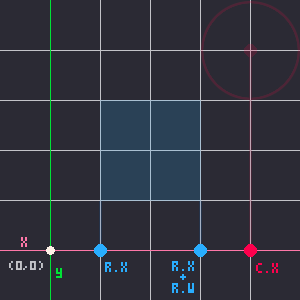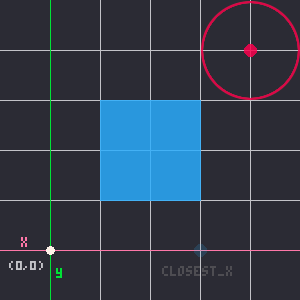
Notice that the middle point in that example is the closest point on the rectangle to the circle's center point. Next, let's consider how many possible positions the rectangle and circle could be, still only on the X axis.

There are only 3 possible positions for the rectangle and circle to be in (in this one axis), and those are:

1. The circle is to the left of the rectangle.

2. The circle is somewhere between the two sides of the rectangle.

3. The circle is to the right of the rectangle.

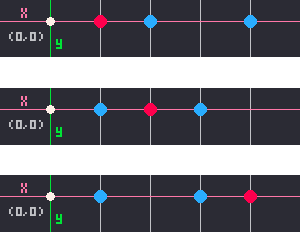
When we look closely at the relationship of the 3 points in those 3 possible positions, you can see that whichever point is in the middle, is the closest point on the rectangle to the circle's center point. Play around with the demo at the top of the page, and click "Show Measurements" to really see why that is true.

The middle point always being the closest point makes it so simple because we already have a function to get the middle number of 3 numbers, mid()!

--get 3 points and find the middle number
circ_center = c.x
rect_left = r.x
rect_right = r.x + r.w

closest_x = mid( circ_center, rect_left, rect_right )

--condenced to just 1 line
closest_x = mid( c.x, r.x, r.x+r.w )

The same is true for the Y axis. We want to find the middle number of the circle's center, c.y, the rectangle's top, r.y, and the rectangle's bottom, r.y+r.h.

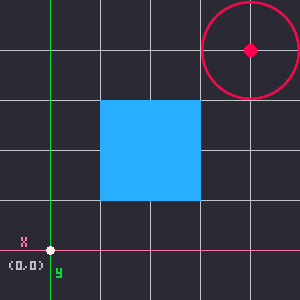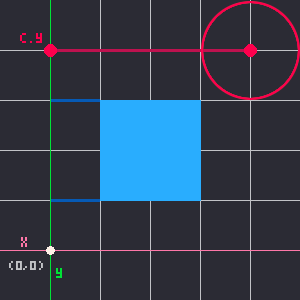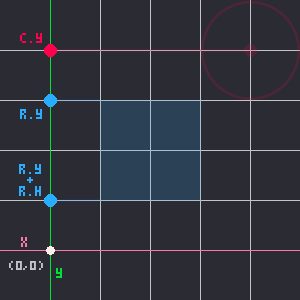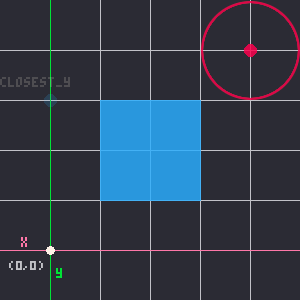
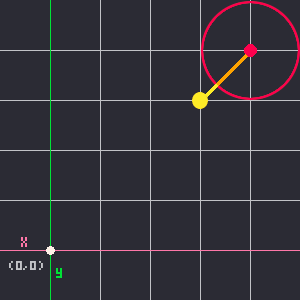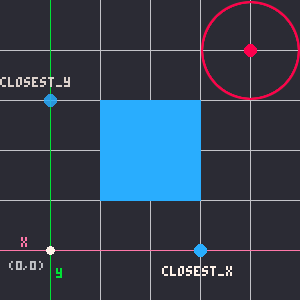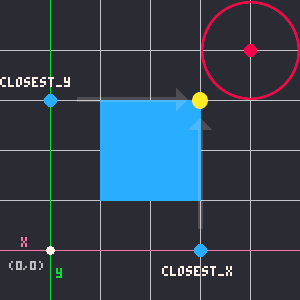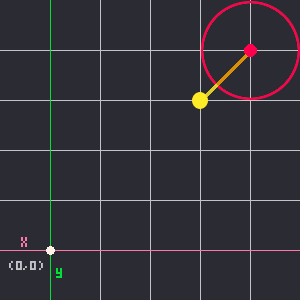
That took a lot of figuring out but this method of finding the middle point on both axes, gives us two simple lines of code:

closest_x = mid( c.x, r.x, r.x+r.w )
closest_y = mid( c.y, r.y, r.y+r.h )

Those two values become the coordinates of the closest point on the rectangle to the circle. And from there, the whole collision problem of these two shapes simplifies down to point-circle collision!

Calculating Distance

The point-circle collision part of this is where we get the distance between the closest point and the circle's center point, then compare that distance with the circle's radius. If the radius is shorter, then the rectangle is outside of the circle, but if the radius is longer that means that the closest point on the rectangle is somewhere inside of the circle, meaning these two shapes overlap!

-- calculate distance from circle center to closest point
distance_x = c.x - closest_x
distance_y = c.y - closest_y
distance_squared = distance_x * distance_x + distance_y * distance_y

-- check if distance is less than or equal to radius
collide = distance_squared <= c.r * c.r

See Point-Circle Collision for more explanation on how the math works to find and compare distance and radius. You'll find it in the section "How it Works" then "Understanding the Math".

Understanding an Expanded Version

Now that we have a rectangle and a circle with coordinates and sizes, and we understand how to figure out the distance between the closest point on the rectangle to the edge of the circle, we can put it all together into an expanded function like this:

--expanded example
function rect_circle_collision(r, c)
  -- find closest point on rectangle to circle center
  local closest_x = mid(c.x, r.x, r.x + r.w)
  local closest_y = mid(c.y, r.y, r.y + r.h)

  -- calculate distance from circle center to closest point
  local distance_x = c.x - closest_x
  local distance_y = c.y - closest_y
  local distance_squared = distance_x * distance_x + distance_y * distance_y

  -- check if distance is less than or equal to radius
  if distance_squared <= c.r * c.r then
		return true
	else
		return false
	end
end

This function has parameters (r,c) and it is expecting those to be objects with coordinates X, Y and size of W and H, or R keys. 

The function first finds the values of the closest X and closest Y on the rectangle to the circle. Then it calculates the distance from that closest point to the center point of the circle. Finally, it checks if the distance is less than or equal to the circle's radius. If so, then it returns true meaning they are colliding, otherwise it returns false, not colliding.

You can call this function in two ways to catch the returned true or false result:

--catch result in variable
is_colliding = rect_circle_collision( r, c )

if is_colliding then
	print( "collided!" )
end

--directly inside of if statement
if rect_circle_collision( r, c ) then
	print( "collided!" )
end

Note that these examples use the same argument names and parameter names just for the convenience of this tutorial, but to make the difference clear, this is how the parameters of the function still uses (r,c) but the arguments when calling the function could be any object table such as:

player = { x=10, y=20, w=8, h=8 }
ball = { x=30, y=40, r=8 }

if rect_circle_collision( player, ball) then
	--player kicks ball
end

(See more examples below in When to Use this?)

Understanding the Simplified Version

We can simplify and condense the expanded version down to just two lines:

function rect_circle_collision(r,c)
	local dx,dy=c.x-mid(c.x,r.x,r.x+r.w),c.y-mid(c.y,r.y,r.y+r.h)
	return dx*dx+dy*dy<=c.r*c.r
end

(This is the same function as under the interactive demo)

This works the exact same way as the expanded version because all the math to find the closest point and calculate distance is being done in the first line, then the comparing of the distance with the radius in the second line will result in either true or false the same way it does in an if statement. So we don't need the if statement at all.

We can just return the result of the distance radius comparison immediately in a single step and it does the same thing as checking: if true return true, else if false return false.

Rectangle to Circle Collision is used quite often in game development, especially in more advanced physics-based games where the main game object is a circle such as sports balls, pinballs, fireballs, or asteroids, and other objects are flat rectangles like walls, ground, bullets, etc. 

Here are a couple classic game examples and where they could use rectangle to circle collision:

Arkanoid's paddle, bricks, and ball

Donkey Kong's player, platforms, and barrels