collision:
Circle to Circle
Circle collision is detected by checking if the distance between their centers is less than the sum of their radii.
No Collision
PICO-8 Collision Function
function circle_circle_collision(c1, c2)
local dx,dy,rsum = c2.x-c1.x, c2.y-c1.y, c1.r+c2.r
return dx*dx+dy*dy <= rsum*rsum
endPreparing Coordinates
First, we need an easy way to store the coordinates of both circles as well as the circles' sizes. We can do that with 2 tables that store separate X, Y, and R (radius) variables. The radius is the distance from the center of the circle to the outer edge. Those tables ( we will name c1 and c2 ) are what the above function expects.
They could be created like this:
--create object tables
c1 = { x=10, y=20, r=20 }
c2 = { x=63, y=63, r=30 }c1 |
|
|---|---|
x |
10 |
y |
20 |
r |
20 |
c2 |
|
|---|---|
x |
63 |
y |
63 |
r |
30 |
Now we have two points at their own coordinates of X and Y, which will be the center points of the circles, and the each circle has a size of r. Next we need to know how to get the values out of the tables. For example, to get the radius of the first circle, we use c1.r (See Table Shorthand).
--get values out of object table
print( c1.r ) --prints 20Understanding the Math
The good news is you don't need to understand the details of how it works in order to use this collision function in your game. As long as you understand what you need to pass to the function and what you can expect to get returned, then you can simply trust that the math inside is working properly.
However, if you want to take more control over your code and customize how your game collision works, then understanding exactly how and why the math works the way it does is important. So we will break it down as best we can.
Overall, we want to get the distance between the two center points by using the coordinates. We'll use some algebra and geometry here to figure out the distance. First we can easily find the difference between each point on each axis. Think of the center point of the circle c1 at ( x1, y1 ) and c2 at ( x2, y2 ).
x2 - x1 = horizontal difference
y2 - y1 = vertical difference
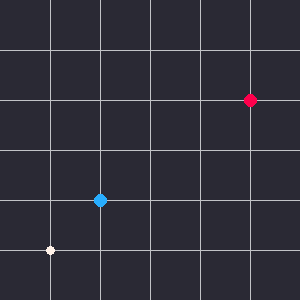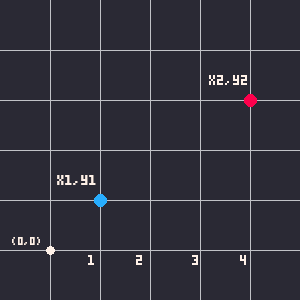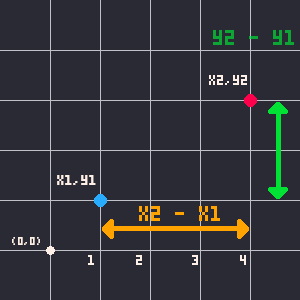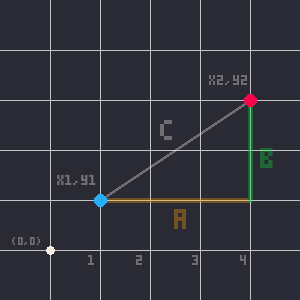
We can do this with any 2 points, imagining them as part of a right triangle, and with just subtraction we get the lengths of 2 sides of that triangle. The 3rd side is the actual distance we want to figure out. Now that we have the lengths of 2 sides of a triangle, we can figure out the third side using the Pythagorean Theorem:
c2 = a2 + b2
Basically it's just a rule about right triangles where the longest side equals the two shorter sides added together, but only when all three sides are multiplied by themselves ("squared").
We can expand that out to look like this:
c×c = a×a + b×b
And this is how we would write it in code:
c*c = a*a + b*b
Applying to our Circles
Let's not get confused when we change from the math where we use A B C for the triangle sides above, back to code where we are using C1 and C2 for the circles again. This is how we do the same but with our point and circle data.
| math | code | |
|---|---|---|
| Difference X = | x2 - x1 | c2.x - c1.x |
| Difference Y = | y2 - y1 | c2.y - c1.y |
In code, we can do that math to get the length of the two smaller sides, and save them in variables named dx and dy.
--difference of points
dx = c2.x - c1.x
dy = c2.y - c1.yThe next step is to multiply those sides by themselves, remember:
c*c = a*a + b*b
Translating this to code, the A is DX and the B is DY, so we want to do:
distance_squared = dx*dx + dy*dyAnd now we could simply square root the result to find the distance:
distance = sqrt( distance_squared )(PICO-8 has a built in math function for this: sqrt)
After we get the distance between the two points, we just need to compare that distance with the two radii of the circles. If the distance between their centers is shorter than the two radii added together, then the circles must be overlapping!
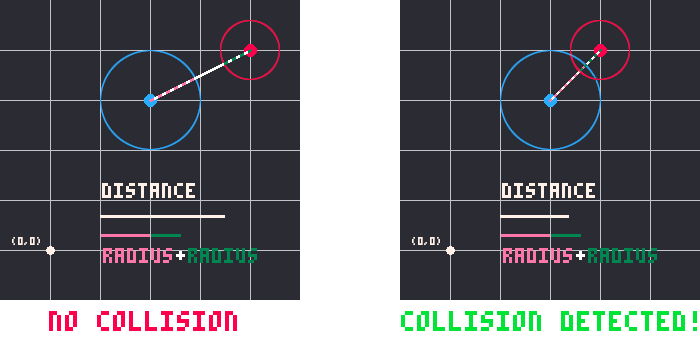
if distance <= c1.r + c2.r then
print( "circles are overlapping!" )
endNow that you understand the math of finding the distance and comparing it with the two radii, play with the demo at the top of this page to see all the pieces come together.
Understanding an Expanded Version
We can combine all of the steps above into a single function, written out clearly to show each step:
function circle_circle_collision( c1, c2 )
--get the differences
local dx = c2.x-c1.x
local dy = c2.y-c1.y
--get the distance
local distance_squared = dx*dx + dy*dy
local distance = sqrt( distance_squared )
--get the sum of radii
local rsum = c1.r + c2.r
--compare distance with radii
if distance <= rsum then
return true
else
return false
end
endThis function has parameters (c1,c2) and it is expecting those to be objects with X, Y, and R keys.
Step 1: get the differences between the center points on each axis, which creates an imaginary right triangle.
Step 2: get the distance of the third side of the triangle, the actual distance of the two points.
Step 3: compare the distance and the circles' radii added together (their sum).
Step 4: return true if the distance is shorter than the sum of the two radii or false if it is longer.
You can call this function in two ways to catch the returned true or false result:
--catch result in variable
is_colliding = circle_circle_collision( c1, c2 )
if is_colliding then
print( "collided!" )
end--directly inside of if statement
if circle_circle_collision( c1, c2 ) then
print( "collided!" )
endNote that these examples use the same argument names and parameter names just for the convenience of this tutorial, but to make the difference clear, this is how the parameters of the function still uses (c1,c2) but the arguments when calling the function could be any object table such as in a pool/billiards/snooker game:
--init
cue_ball = { x=10, y=20 }
balls = {}
add_balls() --creates billiard balls
--update
for ball in all(balls) do
if circle_circle_collision( cue_ball, ball ) then
--apply bounce physics
end
end(See more examples below in When to Use this?)
Understanding the Simplified Version
We can simplify and condense the expanded version down to just two lines:
function circle_circle_collision(c1, c2)
local dx,dy,rsum = c2.x-c1.x, c2.y-c1.y, c1.r+c2.r
return dx*dx+dy*dy <= rsum*rsum
end
This works the exact same way as the expanded version because all the steps of getting the distance and comparing it to the sum of the radii is happening here too.
The first way we condensed the code is what is called multiple assignments. Where we assign more than one value to more than one variable on a single line. That way we assign dx, dy, and rsum together on the first line of the function, separated by commas.
local dx,dy,rsum = c2.x-c1.x, c2.y-c1.y, c1.r+c2.rThe second trick we do to condense the code is to skip saving the distance squared in a variable and then having to square root that to get the distance in another variable. Instead, we do the math for finding the distance squared and immediately compare it with the sum of the circles' radii squared.
dx*dx+dy*dy <= rsum*rsum The final trick to condense it is to simply return the result of the comparison (if the distance squared is less than or equal to the sum of the radii squared), which lets us do all of that in a single line of code. It will do the math first, then compare the two results, then return the comparison's result of true or false.
return dx*dx+dy*dy <= rsum*rsumCircle to Circle Collision is used quite often, obviously when circular game objects are used like balls, rings, hoops, etc, but you might be surprised that it comes in handy even for: non-circular objects; fields of view; or gravity, magnetic, or electric fields; swings and chains, and more. Here are some examples:

Billiards / Pool / Snooker games want to recreate realistic physics with the way the balls bounce off of each other and the sides. Getting this right is really important to the feel of the game. Other sports games such as football (soccer) could have both the ball and the players as circular objects, and the goals rectangular. Pinball is another similar example, where the ball collides with circular bouncers or pins in the middle of the table.

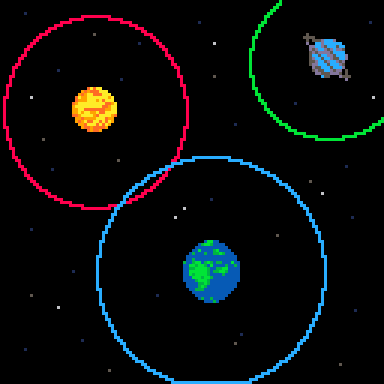
Planetary space games like this may have visible or invisible circular bounds much larger than the planets themselves where their gravity will affect each other. You may even be a tiny ship trying to navigate through all these circle colliders trying not to get pulled in toward the centers where there can be a second smaller circle collider that means destruction. It doesn't have to be space themed either, this idea also applies to games using magnets or electrical fields too.
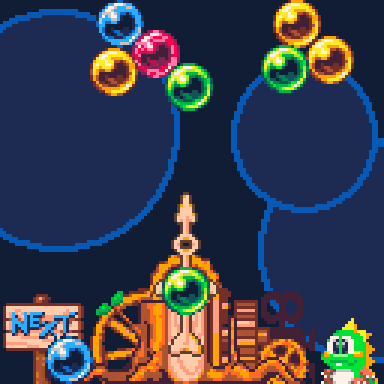
The classics Bust-a-Move and Bubble Bobble both use circular colorful bubbles or marbles that bounce around the screen and interact with each other. Although the objects are all circular and use Circle to Circle collision when moving freely, they also align the bubbles to a grid that is traditionally rectangular or a modern version may use hexagonal grid to stick the bubbles diagonally like this mockup. The point is, collision systems can be a complex mix of shapes that interact and align your game objects the way you want them.
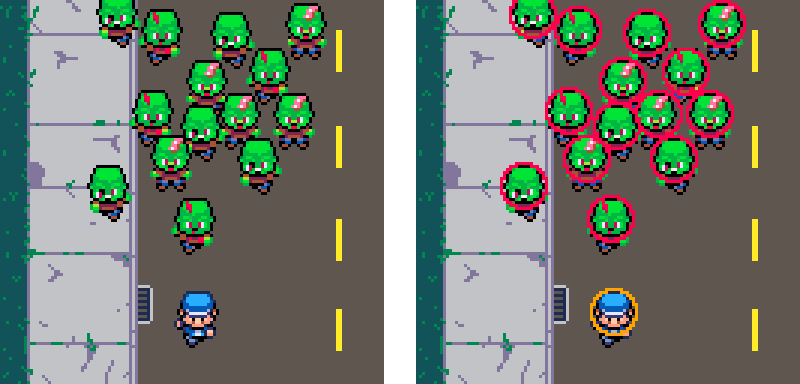
Sometimes you'll have a game where it looks like it should use rectangles for hitboxes and collision, but circles could actually look and feel even better. Here is an example of rectangular sprites in our made-up zombie top-down game.
This mockup (below and on the left) doesn't look bad at all, with the zombies spaced out according to their rectangular hitboxes that cover their entire sprite. This is simple to do in code since both the sprite and the collision hitboxes use the same X, Y, W, H variables. But once you notice that the zombies bump in to each other awkwardly, and keep a perfect distance from each other, you won't be able to unsee it, and the game will just feel "off" somehow.
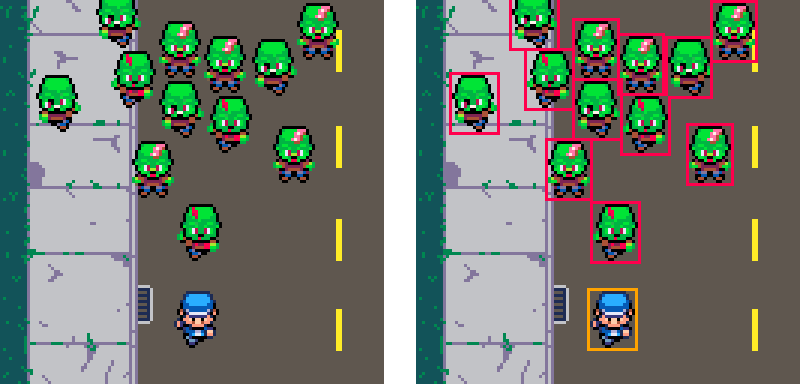
On the other hand, we could change the zombies and player to use circular collision bounds instead, where the lower half of the body is outside of the circle. This allows the zombies to get closer together, bump into each other better, overlap their lower halves, and slide around each other easier. All of that helps the game look and feel more natural and realistic to the player.
2277
16 Apr 2025



